Twierdzenie Talesa

Jeżeli ramiona kąta przecięte są prostymi równoległymi, to odcinki wyznaczone przez te proste na jednym ramieniu kąta, są proporcjonalne do odpowiednich odcinków na drugim ramieniu kąta.

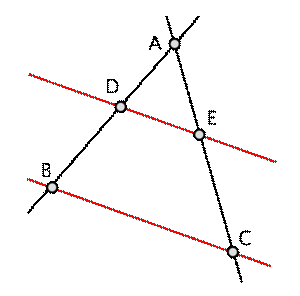
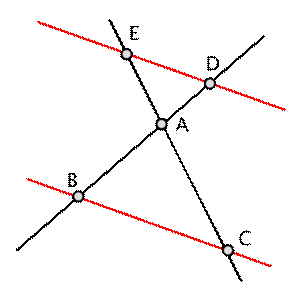Dla powyższych rysunków zachodzi: $\frac{|AD|}{|AE|}=\frac{|DB|}{|EC|}=\frac{|AB|}{|AC|}$

lub po przekształceniu: $\frac{|AE|}{|EC|}=\frac{|AD|}{|DB|}$ oraz $\frac{|AE|}{|AC|}=\frac{|AD|}{|AB|}$ a także $\frac{|AC|}{|EC|}=\frac{|AB|}{|DB|}$ .

Często spotykaną nieścisłością jest takie formułowanie twierdzenia Talesa: $\frac{|AD|}{|DE|}=\frac{|AB|}{|BC|}$ , ta równość jest oczywiście prawdziwa, ale wynika z podobieństwa trójkątów ADE i ABC a nie z samego twierdzenia Talesa.

Twierdzenie odwrotne do twierdzenia Talesa

Jeżeli ramiona kąta przecięte są dwiema prostymi nie pokrywającymi się z tymi ramionami i zachodzi którykolwiek z warunków:

$\frac{|AD|}{|AE|}=\frac{|AB|}{|AC|}$

$\frac{|AE|}{|AC|}=\frac{|AD|}{|AB|}$

gdzie:

A to wierzchołek kąta
Punkty przecięcia pierwszej prostej to B (z pierwszym ramieniem) i C (z drugim ramieniem)
Punkty przecięcia drugiej prostej to D (z pierwszym ramieniem) i E (z drugim ramieniem)

to proste są równoległe.
(Jeśli zachodzi jeden z tych warunków, to drugi również)

Uwaga! Twierdzenie odwrotne do twierdzenia Talesa nie jest w ogólności prawdziwe dla warunków:

$\frac{|DB|}{|EC|}=\frac{|AB|}{|AC|}$

(1)

$\frac{|AC|}{|EC|}=\frac{|AB|}{|DB|}$

(2)

$\frac{|AE|}{|EC|}=\frac{|AD|}{|DB|}$

(3)

$\frac{|AD|}{|AE|}=\frac{|DB|}{|EC|}$

(4)

Warunki te są spełnione dla prostych równoległych (twierdzenie Talesa) ale nie tylko dla nich. Wystarczy wyjść od prostych równoległych i odbić punkt E symetrycznie względem punktu C, a równania (1), (2) i (4) pozostaną spełnione, choć proste nie będą już równoległe. Analogicznie, po odbiciu punktu C wzlędem E, spełnione będą równania (3) i (4).